Deep Residual Shrinkage Network (DRSN) je izboljšana različica globokih rezidualnih mrež (Deep Residual Network). V bistvu gre za integracijo globokih rezidualnih mrež, mehanizmov pozornosti in funkcij mehkega pragovnega krčenja.
Do določene mere lahko delovanje mreže DRSN razumemo takole: z uporabo mehanizmov pozornosti prepozna nepomembne značilke in jih s pomočjo funkcije mehkega pragovnega krčenja postavi na nič; oziroma prepozna pomembne značilke in jih ohrani. S tem se okrepi sposobnost globoke nevronske mreže za izločanje koristnih značilk iz signalov, ki vsebujejo šum.
1. Motivacija za raziskavo
Prvič, pri klasifikaciji vzorcev se ne moremo izogniti prisotnosti določene mere šuma, kot so Gaussov šum, roza šum, Laplaceov šum in podobno. Bolj posplošeno rečeno, vzorci pogosto vsebujejo informacije, ki niso povezane s trenutno nalogo klasifikacije, kar lahko prav tako razumemo kot šum. Ta šum lahko negativno vpliva na uspešnost klasifikacije. (Mehko pragovno krčenje je ključni korak v mnogih algoritmih za razšumljanje signalov).
Na primer, med pogovorom ob cesti se lahko glasovi mešajo z zvoki avtomobilskih hup, koles itd. Pri izvajanju prepoznave govora na teh signalih bodo rezultati neizogibno pod vplivom teh zvokov. Z vidika globokega učenja (Deep Learning) bi bilo treba značilke, ki ustrezajo hupam in kolesom, znotraj globoke nevronske mreže odstraniti, da ne bi vplivale na učinkovitost prepoznave govora.
Drugič, celo znotraj istega nabora podatkov se količina šuma od vzorca do vzorca pogosto razlikuje. (To je podobno mehanizmom pozornosti; če vzamemo za primer nabor slik, se lahko položaj ciljnega predmeta na različnih slikah razlikuje; mehanizem pozornosti se lahko osredotoči na specifičen položaj ciljnega predmeta na vsaki sliki posebej).
Na primer, ko treniramo klasifikator za mačke in pse, imamo 5 slik z oznako “pes”. Prva slika lahko vsebuje psa in miš, druga psa in gos, tretja psa in kokoš, četrta psa in osla, peta pa psa in raco. Pri treniranju klasifikatorja bomo neizogibno podvrženi motnjam zaradi nepomembnih objektov, kot so miši, gosi, kokoši, osli in race, kar povzroči padec natančnosti klasifikacije. Če bi nam uspelo opaziti te nepomembne objekte (miši, gosi, kokoši, osli in race) in odstraniti njim pripadajoče značilke, bi lahko povečali natančnost klasifikatorja za mačke in pse.
2. Mehko pragovno krčenje (Soft Thresholding)
Mehko pragovno krčenje je osrednji korak mnogih algoritmov za razšumljanje signalov. Značilke, katerih absolutna vrednost je manjša od določenega praga, se izbrišejo, tiste z večjo absolutno vrednostjo pa se “skrčijo” proti ničli. To lahko implementiramo z naslednjo formulo:
\[y = \begin{cases} x - \tau & x > \tau \\ 0 & -\tau \le x \le \tau \\ x + \tau & x < -\tau \end{cases}\]Odvod izhoda mehkega pragovnega krčenja glede na vhod je:
\[\frac{\partial y}{\partial x} = \begin{cases} 1 & x > \tau \\ 0 & -\tau \le x \le \tau \\ 1 & x < -\tau \end{cases}\]Kot je razvidno zgoraj, je odvod mehkega pragovnega krčenja bodisi 1 bodisi 0. Ta lastnost je enaka kot pri aktivacijski funkciji ReLU. Zato lahko mehko pragovno krčenje prav tako zmanjša tveganje, da bi v algoritmih globokega učenja prišlo do problema izginjanja (gradient vanishing) ali eksplozije gradienta (gradient exploding).
Pri funkciji mehkega pragovnega krčenja mora nastavitev praga izpolnjevati dva pogoja: prvič, prag mora biti pozitivno število; drugič, prag ne sme biti večji od maksimalne vrednosti vhodnega signala, sicer bi bil izhod v celoti enak nič.
Hkrati je zaželeno, da prag izpolnjuje še tretji pogoj: vsak vzorec bi moral imeti svoj neodvisen prag, ki temelji na lastni vsebnosti šuma.
To pa zato, ker se vsebnost šuma med vzorci pogosto razlikuje. Znotraj istega nabora podatkov se pogosto zgodi, da vzorec A vsebuje manj šuma, vzorec B pa več. Če v tem primeru izvajamo mehko pragovno krčenje v algoritmu za razšumljanje, bi moral vzorec A uporabiti nižji prag, vzorec B pa višjega. V globokih nevronskih mrežah te značilke in pragovi sicer izgubijo jasen fizikalni pomen, vendar osnovna logika ostaja enaka. Z drugimi besedami, vsak vzorec bi moral imeti svoj neodvisen prag, določen glede na specifično vsebnost šuma v tem vzorcu.
3. Mehanizem pozornosti (Attention Mechanism)
Mehanizme pozornosti je na področju računalniškega vida (Computer Vision) precej enostavno razumeti. Vizualni sistem živali lahko hitro pregleda celotno območje in odkrije ciljni predmet, nato pa pozornost usmeri nanj, da izlušči več podrobnosti, hkrati pa zatre nepomembne informacije. Za podrobnosti glejte literaturo s področja mehanizmov pozornosti.
Squeeze-and-Excitation Network (SENet) je novejša metoda globokega učenja, ki uporablja mehanizme pozornosti. Pri različnih vzorcih je prispevek različnih kanalov značilk (feature channels) h klasifikacijski nalogi pogosto različen. SENet uporablja majhno podmrežo za pridobitev niza uteži, nato pa te uteži pomnoži z značilkami posameznih kanalov, da prilagodi velikost značilk v vsakem kanalu. Ta proces lahko razumemo kot uporabo različnih stopenj pozornosti na različnih kanalih značilk.
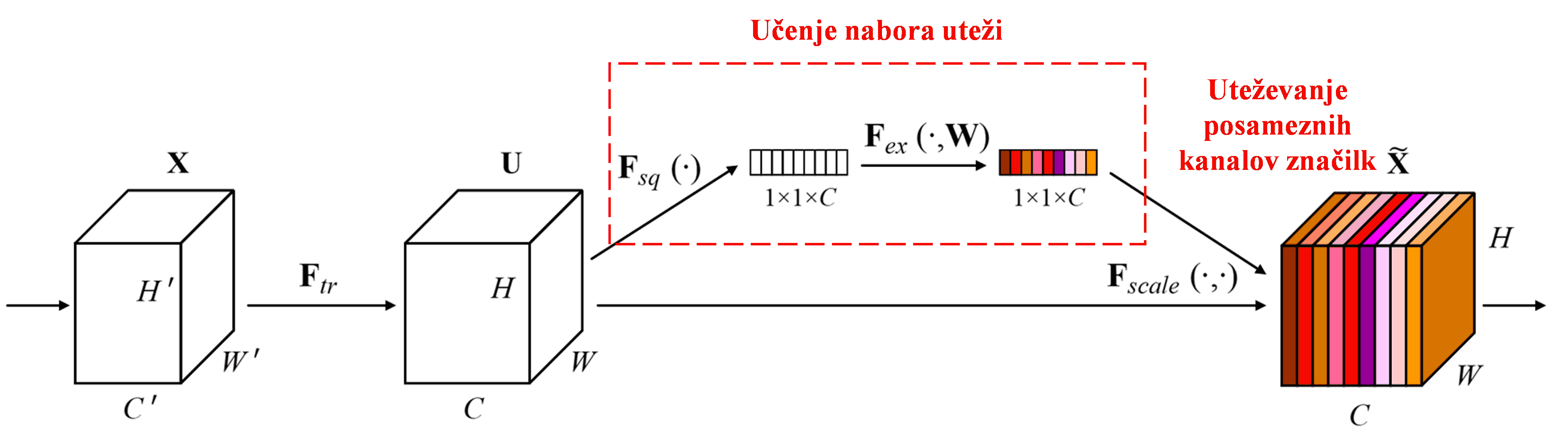
Na ta način ima vsak vzorec svojo neodvisno skupino uteži. Z drugimi besedami, uteži dveh poljubnih vzorcev sta različni. V SENet je pot za pridobitev uteži naslednja: “Globalno združevanje (global pooling) → Polno povezana plast → ReLU funkcija → Polno povezana plast → Sigmoid funkcija”.
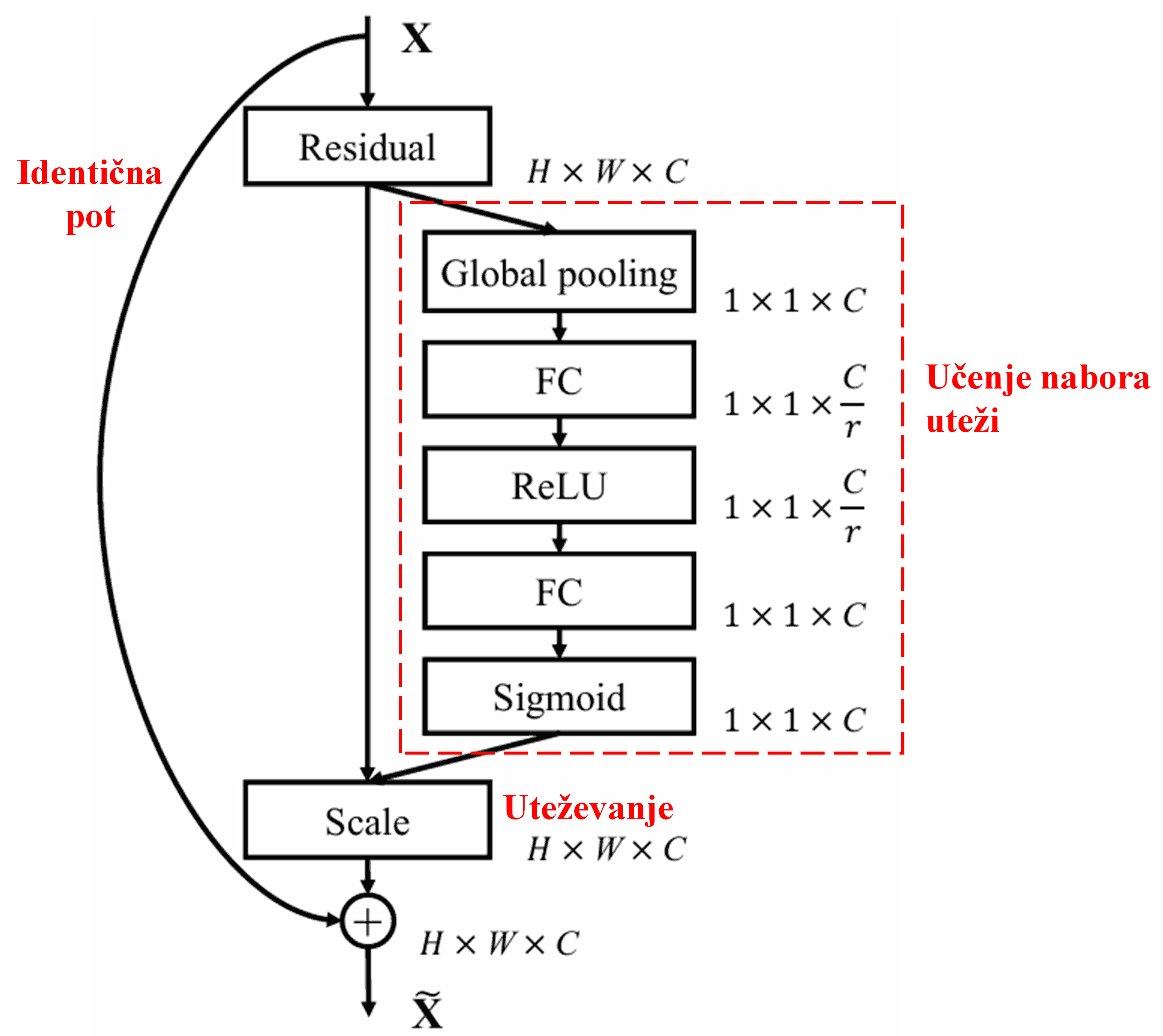
4. Mehko pragovno krčenje z globokim mehanizmom pozornosti
Deep Residual Shrinkage Network (DRSN) si izposoja omenjeno strukturo podmreže SENet za implementacijo mehkega pragovnega krčenja s pomočjo globokega mehanizma pozornosti. Skozi podmrežo (označeno z rdečim okvirjem) se lahko naučimo nabora pragov za izvedbo mehkega pragovnega krčenja na vsakem kanalu značilk.
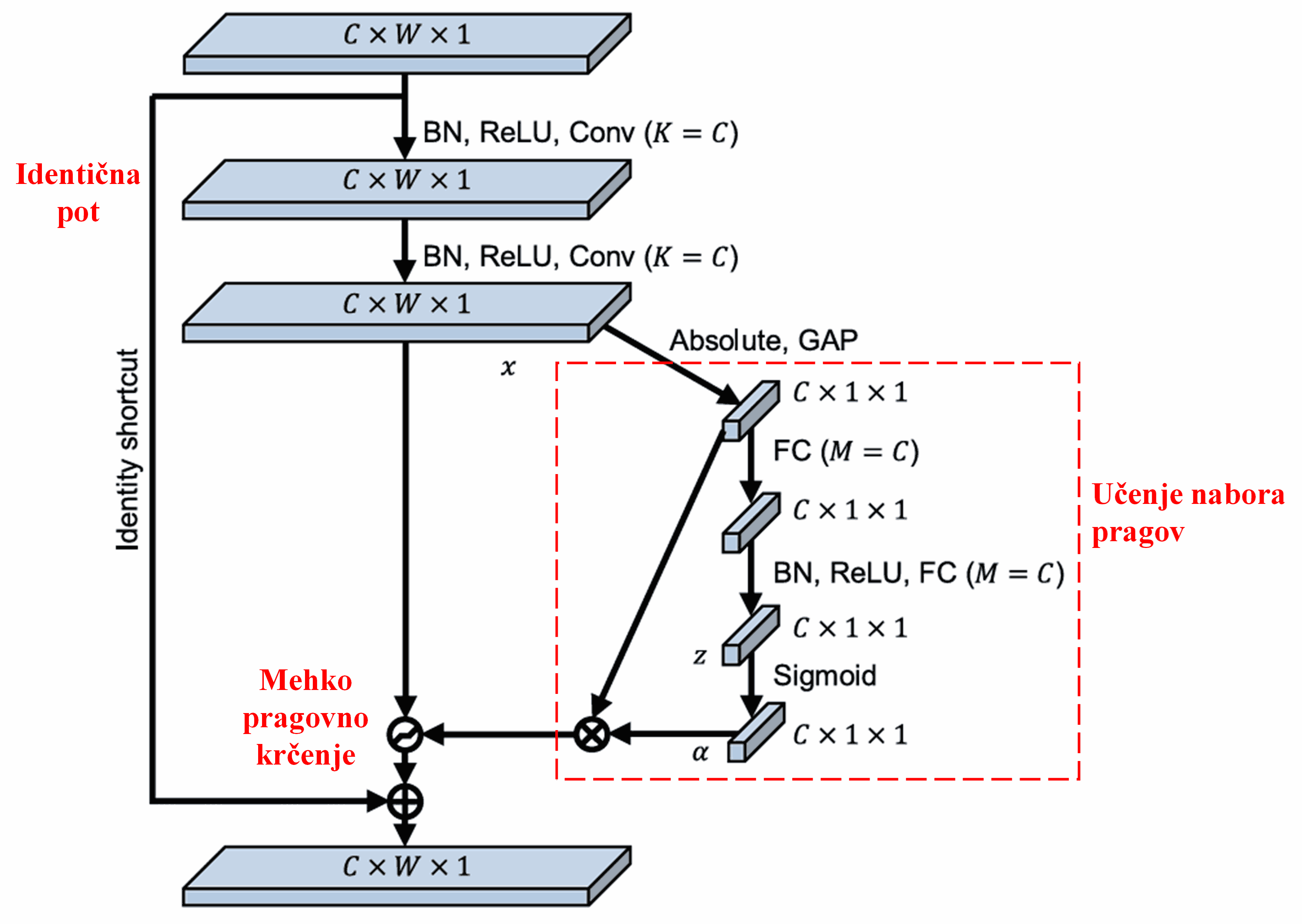
V tej podmreži se najprej izračuna absolutna vrednost vseh značilk vhodne mape značilk (feature map). Nato se s pomočjo globalnega povprečnega združevanja (global average pooling) in povprečenja pridobi značilka, ki jo označimo z A. V drugi poti se mapa značilk po globalnem povprečnem združevanju vnese v majhno polno povezano mrežo. Ta polno povezana mreža uporablja funkcijo Sigmoid kot zadnjo plast, da normalizira izhod na vrednost med 0 in 1, s čimer dobimo koeficient, ki ga označimo z α. Končni prag lahko zapišemo kot α × A. Torej je prag produkt števila med 0 in 1 ter povprečja absolutnih vrednosti mape značilk. Ta način ne zagotavlja le, da je prag pozitiven, ampak tudi, da ni prevelik.
Poleg tega imajo različni vzorci različne pragove. Zato lahko to do določene mere razumemo kot poseben mehanizem pozornosti: omrežje opazi značilke, ki niso pomembne za trenutno nalogo, jih skozi dve konvolucijski plasti pretvori v vrednosti blizu 0 in jih s pomočjo mehkega pragovnega krčenja postavi na nič; oziroma opazi pomembne značilke, povezanih s trenutno nalogo, jih skozi dve konvolucijski plasti pretvori v vrednosti daleč od 0 in jih ohrani.
Na koncu z zlaganjem določenega števila osnovnih modulov ter konvolucijskih plasti, paketne normalizacije (batch normalization), aktivacijskih funkcij, globalnega povprečnega združevanja in polno povezane izhodne plasti dobimo celotno mrežo DRSN.
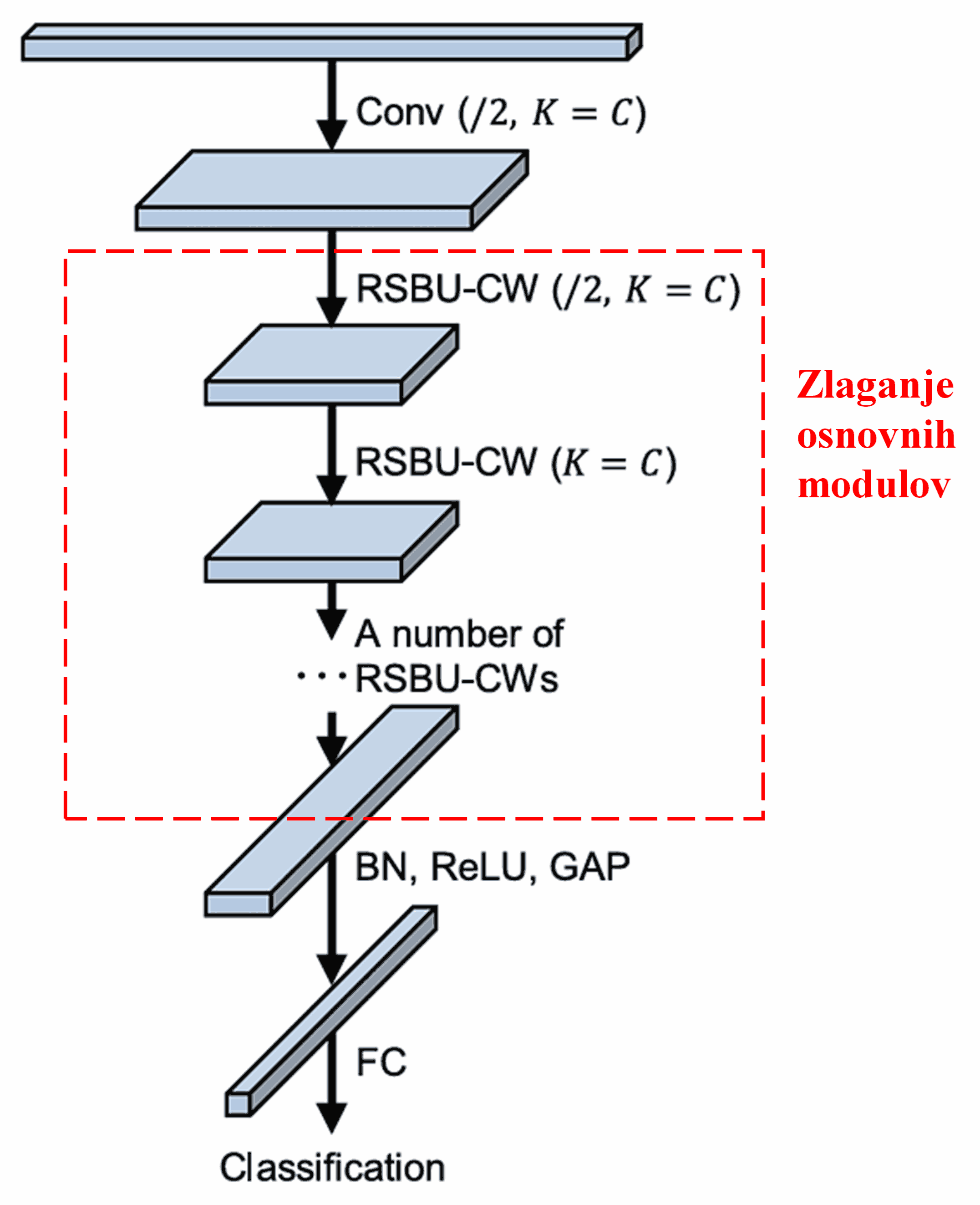
5. Splošna uporabnost
Deep Residual Shrinkage Network je pravzaprav splošna metoda za učenje značilk. To pa zato, ker pri mnogih nalogah učenja značilk vzorci bolj ali manj vsebujejo nekaj šuma in nepomembnih informacij. Ta šum in nepomembne informacije lahko vplivajo na učinkovitost učenja značilk. Na primer:
Pri klasifikaciji slik, če slika hkrati vsebuje veliko drugih predmetov, lahko te predmete razumemo kot “šum”. Deep Residual Shrinkage Network lahko s pomočjo mehanizma pozornosti opazi ta “šum” in nato s pomočjo mehkega pragovnega krčenja značilke, ki ustrezajo temu “šumu”, postavi na nič, kar lahko poveča natančnost klasifikacije slik.
Pri prepoznavanju govora, še posebej v okoljih z veliko hrupa, na primer med pogovorom ob cesti ali v tovarniški hali, lahko Deep Residual Shrinkage Network izboljša natančnost prepoznave govora ali vsaj ponudi pristop, ki omogoča izboljšanje natančnosti.
Reference:
Minghang Zhao, Shisheng Zhong, Xuyun Fu, Baoping Tang, Michael Pecht, Deep residual shrinkage networks for fault diagnosis, IEEE Transactions on Industrial Informatics, 2020, 16(7): 4681-4690.
https://ieeexplore.ieee.org/document/8850096
BibTeX
@article{Zhao2020,
author = {Minghang Zhao and Shisheng Zhong and Xuyun Fu and Baoping Tang and Michael Pecht},
title = {Deep Residual Shrinkage Networks for Fault Diagnosis},
journal = {IEEE Transactions on Industrial Informatics},
year = {2020},
volume = {16},
number = {7},
pages = {4681-4690},
doi = {10.1109/TII.2019.2943898}
}
Vpliv in citiranost
Članek ima na Google Scholar že več kot 1400 citatov.
Po nepopolnih statističnih podatkih je bila mreža Deep Residual Shrinkage Network (DRSN) uporabljena ali izboljšana v več kot 1000 publikacijah na številnih področjih, vključno s strojništvom, energetiko, računalniškim vidom, medicino, obdelavo govora, obdelavo besedil, radarji in daljinskim zaznavanjem.